Quotient space
In topology and related areas of mathematics, a quotient space (also called an identification space) is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation. This is commonly done in order to construct new spaces from given ones.
Contents |
Definition
Let (X,τX) be a topological space, and let ~ be an equivalence relation on X. The quotient space,  is defined to be the set of equivalence classes of elements of X:
is defined to be the set of equivalence classes of elements of X:
equipped with the topology where the open sets are defined to be those sets of equivalence classes whose unions are open sets in X:
Equivalently, we can define them to be those sets with an open preimage under the quotient map  which sends a point in X to the equivalence class containing it.
which sends a point in X to the equivalence class containing it.
The quotient topology is the final topology on the quotient space with respect to the quotient map.
Examples
- Gluing. Often, topologists talk of gluing points together. If X is a topological space and points
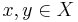 are to be "glued", then what is meant is that we are to consider the quotient space obtained from the equivalence relation a ~ b if and only if a = b or a = x, b = y (or a = y, b = x). The two points are henceforth interpreted as one point.
are to be "glued", then what is meant is that we are to consider the quotient space obtained from the equivalence relation a ~ b if and only if a = b or a = x, b = y (or a = y, b = x). The two points are henceforth interpreted as one point. - Consider the unit square I2 = [0,1]×[0,1] and the equivalence relation ~ generated by the requirement that all boundary points be equivalent, thus identifying all boundary points to a single equivalence class. Then I2/~ is homeomorphic to the unit sphere S2.
- Adjunction space. More generally, suppose X is a space and A is a subspace of X. One can identify all points in A to a single equivalence class and leave points outside of A equivalent only to themselves. The resulting quotient space is denoted X/A. The 2-sphere is then homeomorphic to the unit disc with its boundary identified to a single point: D2/∂D2.
- Consider the set X = R of all real numbers with the ordinary topology, and write x ~ y if and only if x−y is an integer. Then the quotient space X/~ is homeomorphic to the unit circle S1 via the homeomorphism which sends the equivalence class of x to exp(2πix).
- A vast generalization of the previous example is the following: Suppose a topological group G acts continuously on a space X. One can form an equivalence relation on X by saying points are equivalent if and only if they lie in the same orbit. The quotient space under this relation is called the orbit space, denoted X/G. In the previous example G = Z acts on R by translation. The orbit space R/Z is homeomorphic to S1.
Warning: The notation R/Z is somewhat ambiguous. If Z is understood to be a group acting on R then the quotient is the circle. However, if Z is thought of as a subspace of R, then the quotient is an infinite bouquet of circles joined at a single point.
Properties
Quotient maps q : X → Y are characterized among surjective maps by the following property: if Z is any topological space and f : Y → Z is any function, then f is continuous if and only if f O q is continuous.
The quotient space X/~ together with the quotient map q : X → X/~ is characterized by the following universal property: if g : X → Z is a continuous map such that a~b implies g(a)=g(b) for all a and b in X, then there exists a unique continuous map f : X/~ → Z such that g = f O q. We say that g descends to the quotient.
The continuous maps defined on X/~ are therefore precisely those maps which arise from continuous maps defined on X that respect the equivalence relation (in the sense that they send equivalent elements to the same image). This criterion is constantly used when studying quotient spaces.
Given a continuous surjection f : X → Y it is useful to have criteria by which one can determine if f is a quotient map. Two sufficient criteria are that f be open or closed. Note that these conditions are only sufficient, not necessary. It is easy to construct examples of quotient maps which are neither open nor closed.
Compatibility with other topological notions
- Separation
- In general, quotient spaces are ill-behaved with respect to separation axioms. The separation properties of X need not be inherited by X/~, and X/~ may have separation properties not shared by X.
- X/~ is a T1 space if and only if every equivalence class of ~ is closed in X.
- If the quotient map is open then X/~ is a Hausdorff space if and only if ~ is a closed subset of the product space X×X.
- Connectedness
- If a space is connected or path connected, then so are all its quotient spaces.
- A quotient space of a simply connected or contractible space need not share those properties.
- Compactness
- If a space is compact, then so are all its quotient spaces.
- A quotient space of a locally compact space need not be locally compact.
- Dimension
- The topological dimension of a quotient space can be more (as well as less) than the dimension of the original space; space-filling curves provide such examples.
See also
Topology
- Topological space
- Subspace (topology)
- Product space
- Disjoint union (topology)
- Final topology
- Mapping cone
Algebra
References
- Willard, Stephen (1970). General Topology. Reading, MA: Addison-Wesley. ISBN 0-486-43479-6.
- Quotient space on PlanetMath
![Y = \{ [x]�: x \in X \} = \{\{v \in X�: v \sim x\}�: x \in X\},](/2012-wikipedia_en_all_nopic_01_2012/I/6c3d8f68ad0c93f37b53864763d56cda.png)

